- About
- Solutions
- Governance
- Investors
- Sustainability
- Sustainability
- Newsroom
- Jobs
Freeze lining (FL), a protective layer of solidified slag, holds significant economic value in industrial processes. It protects furnaces and refractory linings from corrosive molten slag and acts as a thermal barrier to minimise energy consumption. To improve our understanding of FL formation, an international collaboration was established. It united academic researchers from the Universities of Leoben (Austria) and Leuven (Belgium) with industry partners RHI Magnesita and Aurubis-Beerse. This collaborative effort has led to the development of a novel computational fluid dynamics (CFD) model capable of simulating FL formation across various applications. Extensive validation confirmed the model’s robustness and versatility. This model provides a solid foundation for further fundamental research on FL formation and paves the way for more efficient and cost-effective industrial processes.
In the high-temperature world of pyrometallurgy, furnaces often rely on a self-forming protective layer called freeze lining (FL). FL technology has proven successful in various industrial processes, including copper, lead, and ilmenite smelting, zinc fuming, aluminium production (Hall-Heroult process), and in steelmaking [1–7]. However, despite its proven industrial importance, the mechanisms governing FL formation are not fully understood. While laboratory experiments have provided valuable insights into FL microstructure development and growth characteristics, current models haven’t been able to comprehensively capture these findings. To bridge this gap, a collaborative research project was undertaken to develop a computational fluid dynamics (CFD) model framework capable of simulating FL formation based on prevalent knowledge. The model was validated against a laboratory experiment (i.e., finger experiment) and industrial processes (i.e., electric smelting furnace and slag fuming furnace).
To analyse FL formation under controlled conditions, a laboratory experiment, also known as the finger experiment, was conducted at KU Leuven (Figure 1a). This experiment involved introducing a gas-cooled probe into a slag bath, inducing FL formation that grew outward from the probe’s surface over time. The crucible containing the slag could be set to static (natural convection) or rotating (forced convection) conditions. During the experiment, the slag bath temperature before and during probe immersion, FL thickness over time, and heat fluxes were monitored. The CFD results of the equivalent experimental setup are illustrated in Figure 1b and depict the simulated solid fraction distribution (fs) at three different moments during immersion of the probe into the slag and the FL shape evolution over time. The colour gradient varies from dark blue for the molten slag (also set as transparent in the outer regions), transitioning to a mushy zone (partially solidified slag), and ending with dark red for fully solidified slag (FL). Figure 1c compares the evolution of the measured FL thickness with the simulation results and demonstrates a good quantitative agreement. This validation confirmed the model’s accuracy in a controlled environment.
This case represents an industrial electric smelting furnace for the smelting of nickel matte. The furnace is equipped with six electrodes. A schematic of the cross-sectional view of the furnace (through one of the electrodes) is shown in Figure 2. During operation, the electrical energy for smelting the feed is generated by joule heating as the electric current passes between the carbon electrodes and the molten slag bath. After the furnace is charged with the feed, the process produces both slag and a denser nickel-rich layer called matte, which settles at the bottom due to its higher density. The furnace walls incorporate a cooling system (e.g., water-cooled panels) that promotes the FL formation on the interior surface of the furnace/refractory.
A crucial aspect of modelling the electric smelting furnace involves establishing a valid global energy balance within the furnace. This balance must consider all relevant heat transfer mechanisms occurring during the smelting process. To capture these mechanisms, several energy source terms were incorporated. These terms account for the input power from the electrodes, heat generated from matte production, heat dissipated by the cooling system, heat dissipated by the presence of the feed, and latent heat released during FL formation.
Figure 3 presents the simulation results obtained after reaching a steady state. This means that a thermal balance was achieved in the system. Due to symmetry in the furnace, only one section containing half of one electrode is considered in the model. Figures 3a–3c show the temperature distribution in the section considered, the temperature distribution in a 2D plane intersecting the electrode, and the velocity distribution in a similar 2D plane. The inset in Figure 3a highlights the FL layer formed on the water-cooled wall (black vertical rendering), while the horizontal black rendering corresponds to the solid feed. Figure 3b confirms that the slag temperature is higher closer to the electrode and decreases with distance. This provides the driving force for natural convection in the molten slag. Figure 3c shows an anticlockwise flow pattern in the slag region driven by joule heating. The maximum velocity is approximately 0.05 m/s. These results agree with the plant data reported [9]. The vertical black structure illustrated in the inset of Figure 3a confirms the presence of a FL layer on the water-cooled wall. The results go beyond validating FL formation; they demonstrate the successful integration of key physical phenomena into the model’s framework.
The simulations revealed a critical dependence of the FL layer on heat transfer terms. Notably, variations in feed size were clearly associated with different FL thicknesses. Therefore, an accurate estimation of the thermal effect of the feed is critical and must be considered in the global energy balance calculations of the furnace.
![<p><strong>Figure 3. </strong>Steady-state simulation results of (a) temperature distribution in a section of the domain with an inset showing black rendering corresponding to the FL layer on the water-cooled wall predicted by the model and the feed, (b) temperature distribution with isotherms in a 2D plane intersecting the electrode, and (c) velocity distribution with velocity vectors in a 2D plane intersecting the electrode [8].</p>](https://www.rhimagnesita.com/wp-content/uploads/2024/11/bulletin-2024-1-97-wu-fig-03-241029-1024x591.jpg)
Figure 3. Steady-state simulation results of (a) temperature distribution in a section of the domain with an inset showing black rendering corresponding to the FL layer on the water-cooled wall predicted by the model and the feed, (b) temperature distribution with isotherms in a 2D plane intersecting the electrode, and (c) velocity distribution with velocity vectors in a 2D plane intersecting the electrode [8].
Aurubis-Beerse operates a zinc recovery process called slag fuming (Figure 4). This innovative technique recycles zinc from various industrial waste materials by relying on submerged plasma torches for a carbon-free energy source. Three of these torches transform compressed air into high-temperature plasma. This plasma is then injected into the molten slag bath, along with a mixture of natural gas and pulverised coal. This gaseous mixture acts as a heat source, stirring force, and reducing agent in the fuming process. These zinc fumes are then captured in a baghouse after exiting the furnace. To protect the furnace and its refractory linings from the corrosive molten slag, water-cooled jackets are employed around the furnace to promote FL formation. Crucially, industrial data provided by Aurubis-Beerse played a key role in setting up and validating the model. Since the furnace design is symmetrical, only one-third of it needs to be considered in the model.
The flow dynamics observed during the slag fuming process are shown in Figure 5a. The blue iso-surface, representing the slag/gas interface, illustrates the splashing motion of the molten slag across the freeboard. The splashing events are caused by the interaction between the hot gas plumes (created upon injection through the submerged plasma torches) and the molten slag bath. Four coloured streamlines illustrate the complex slag flow pattern, which is driven by the hot gas injection, plume motion, and their interactions with the splashing events. Arrows on each streamline indicate the flow direction. Notably, the streamlines reach most regions of the 3D domain, which confirm the chaotic flow behaviour in the slag bath.
Figure 5b shows the dynamic interplay between splashing and solidification of the FL layer. It captures a moment just after a previously splashed molten slag layer has solidified in the upper right side of the freeboard. This is confirmed by the solid fraction (fs) colour contour in cyan (which means that it is partially solidified at this moment) and is highlighted in the inset of Figure 5b. This solidification is driven by the heat transfer from the existing, cooler FL layer on the freeboard wall. In contrast, the upper left side of the freeboard shows a fresh splashing event where the slag remains molten (dark blue iso-surface). Figure 6a and 6b show the simulation results of the FL distribution on the reactor wall, and variation of the FL thickness along the reactor height for three angles (φ): 0°, 22°, and 45°.

Figure 5. (a) slag splashing and flow dynamics in the slag bath at t = 180.1 seconds. The blue iso-surface depicts the slag/gas interface. The coloured streamlines illustrate the flow patterns. (b) splashing and FL formation in the freeboard at t = 173.9 seconds. The iso-surface colour contour shows the solid fraction (fs). The inset provides a magnified view of the impact region where splashed slag solidifies.
In the industrial furnace operated by Aurubis-Beerse, the average measured FL thickness was 3 cm. In the slag bath region (height range between 0 and 2 m in Figure 6b), the simulation results show good agreement with industrial data, particularly in regions farther from the submerged plasma torches (φ = 22° and 45°). When φ = 0°, the FL thickness is underestimated because of the simplification made in modelling the submerged plasma torches’ inlet (to reduce computational cost). In the freeboard region (height range between 2 and 5.5 m in Figure 6b), the simulation results align reasonably well with the industrial data in the regions where enough splashing events have occurred. However, in regions with fewer splashing events, the model underestimates FL formation. Splashing is more frequent near the centreline of the furnace (φ = 0°) and reduces as the distance from the centre increases (higher φ values), as observed in Figures 6a and 6b. To achieve a complete FL layer across the entire freeboard surface, industrial furnaces typically employ a special operation regime that was not included in the simulation.
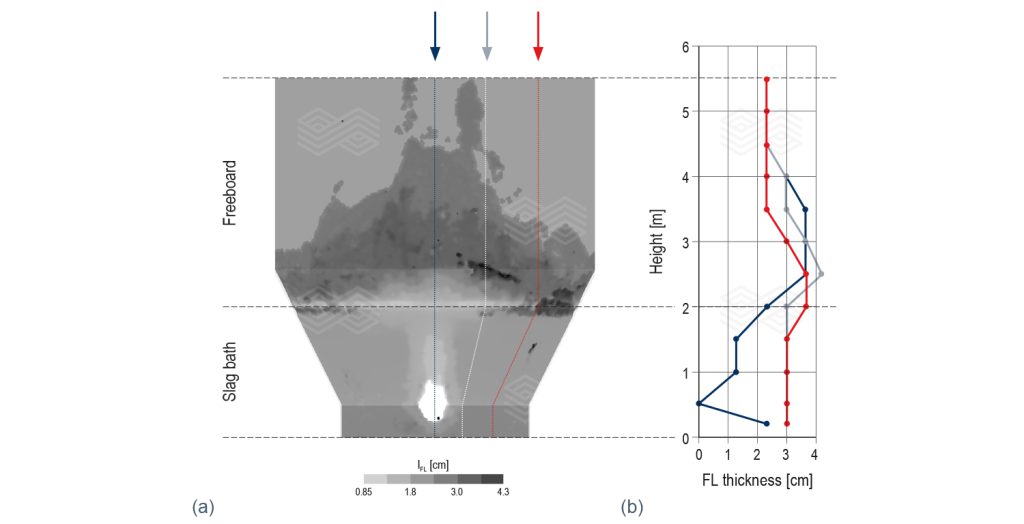
Figure 6. (a) FL distribution across the reactor wall and (b) FL thickness variation along the reactor height for three azimuthal angles (φ): 45°, 22°, 0°. The 0° azimuthal angle corresponds to the vertical plane intersecting the centre of the submerged plasma torches. The average measured FL thickness in the industrial furnace operated by Aurubis-Beerse was 3 cm.
Predicting FL formation remains a significant challenge due to the complex interplay of physical and chemical processes. Modelling offers a powerful tool to unravel these mechanisms. This paper explores the results of a collaborative effort between academia and industry, aiming to develop a comprehensive CFD model for simulating FL formation. The positive agreement between simulations and experimental/industrial data validates the model’s accuracy and the success of the collaboration: Academia’s theoretical expertise combined effectively with industry’s real-world knowledge. However, the current model needs further development. Future work should include incorporating new fundamental knowledge of FL formation kinetics, its response to thermal and compositional fluctuations, and modelling the mobile phase (microstructure) observed in some experiments. Additionally, validation in a wider range of industrial applications will enhance the model’s robustness.
This study was supported by the Austrian Research Promotion Agency (FFG) under the framework of Bridge 1 program (MoSSoFreez Project, F0999888120).
[1] Guevara, F. and Irons, G. Simulation of Slag Freeze Layer Formation: Part I. Experimental Study. Metall. Mater. Trans. B. 2011, 42, 652–663.
[2] Campforts, M., Verscheure, K., Boydens, E., Van Rompaey, T., Blanpain, B. and Wollants, P. On the Mass Transport and the Crystal Growth in a Freeze Lining of an Industrial Nonferrous Slag. Metall. Mater. Trans. B. 2008, 39, 408–417.
[3] Swinbourne, D. The Extractive Metallurgy of Lead. Miner. Process Extr. Metall. 2010, 119, 182.
[4] Zietsman, J. and Pistorius, P. Modelling of an Ilmenite-Smelting DC Arc Furnace Process. Minerals Engineering. 2006, 19, 262–279.
[5] Verscheure, K., Van Camp, M., Blanpain, B., Wollants, P., Hayes, P. and Jak, E. Continuous Fuming of Zinc-Bearing Residues: Part II. The Submerged-Plasma Zinc-Fuming Process. Metall. Mater. Trans. B. 2007, 38, 21–33.
[6] Wong, C., Bao, J., Skyllas-Kazacos, M., Welch, B., Mahmoud, M., Arkhipov, A., and Ahli, N. Studies on Power Modulation of Aluminum Smelting Cells Based on a Discretized Mass and Thermal Dynamic Model. Metall. Mater. Trans. B. 2023, 54, 562–577.
[7] Mills, K., Su, Y., Fox, A., Li, Z., Thackray, R. and Tsai, H. A Review of Slag Splashing. ISIJ Int. 2005, 45, 619–633.
[8] Rodrigues, C., Menghuai, W., Ishmurzin, A., Hackl, G., Voller, N., Ludwig, A. and Kharicha, A. Modeling Framework for the Simulation of an Electric Smelting Furnace Considering Freeze Lining Formation. Metall. Mater. Trans. B. 2023, 54, 880–894.
[9] Sheng, Y., Irons, G. and Tisdale, D. Transport Phenomena in Electric Smelting of Nickel Matte: Part II. Mathematical Modeling. Metall. Mater. Trans. B. 1998, 29, 85–94.